|
Part 1
Digital Jargon - What's It About?
Bits & Bytes To Digital Recording
By William Williams
Voice Actor & Coach
Aliso Creek Productions
Uh, how's that again?
OK, you've performed your first voice over gig from you home voice over studio, and it's time to deliver your performance to your client. Back in the day, you would mix it down to quarter inch tape and FedEx it for next day delivery.
But, whoa!, that was in the last century! Today tape has gone the the way of M C Hammer pants - everything's digital.
And you need to learn the lingo - and moreover, the concepts represented by these words - to communicate effectively with your clients and deliver your work in the format that they require.
So you need to understand and speak digital.
WHAT IS DIGITAL RECORDING?
If you already know this stuff, you can skip this part.
But if you're not sure, clear your mind and settle in 'cause I'm going to explain digital recording once again.
So what is digital recording? Wait a minute ... for that matter what is digital? Let's start with that.
DONE IN DIGITS
Representing information in a digital format came out of the computer industry.
Computers store information with little switches just like the light switch on the wall. That on-the-wall light switch only has two states - it can be ON or OFF.
These two states can be represented with just two digits - a zero (0) for OFF, and a one (1) for ON.
THE BINARY BASE
In everyday life we use a base 10 number system, which uses 10 digits (0,1,2,3,4,5,6,7,8,9) to represent any number.
Ahhh, but what if you only have two digits?
Well, to represent numbers with two digits you need to use a different number system - a base two number system. This is the renowned binary number system.
There have been thousands of articles describing how binary number work, but suffice it to say that we can represent a (base ten) number like 1,362,478 with a binary number like 101001100101000101110.
And that representation of the number can be stored in those little light switches ...on, off, on, off, off, on, on...
OK, you get the idea.
GET THE BIT
By the way, each of the ones or zeros is called a Binary Digit. And since they're little tiny things - and because technical jargon often has some word humor in it - this term got shortened to Bit.
NOW THE BYTE
These binary digits were often worked on in groups or "words" of eight bits. So if you had one group, you would have "one word by eight bits;" six words would be "six words by eight bits."
Well, it didn't take long for those merry computer folks to shorten "by eight" to byte. Get it? Like bite! A bit and a byte.
(And four bits was called a nibble, but you'll rarely hear that term anymore.)
Yeah, those computer labs are a virtual Comedy Store.
RECORDING DIGITALLY
So now you have a number system that you can store in a computer's memory. But how do you convert sound into numbers? Let's start with a quick analogy.
 Suppose we want to map the peaks and valleys of a mountain range. One way to do this would to be to walk along in a straight line and every few feet, take an altitude measurement.
Walk 10 feet, measure: 5,234 feet. Walk 10 feet, measure 5245 feet. Walk 10 feet, measure 5251 feet, and so forth for the whole mountain range.
This would give you a series of numbers - 5234, 5245, 5251) - or in binary, 1010001110010, 1010001111101, 1010010000011, which you can save in your computer.
And by recalling these numbers, you can redraw the peaks and valleys of the mountains.
SOUND WAVE, TOO
Now let's look at a sound wave.
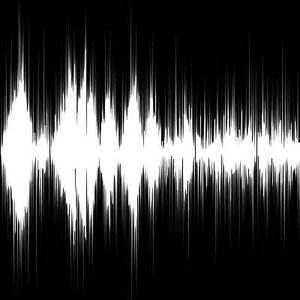 Here's typical audio sound wave. Wow! That looks just like a mountain range. Well, at least a mountain range reflected in a tranquil alpine lake.We can measure the sound wave in a similar way.
Move along a wee bit from left to right (which is the TIME axis), and every few moments take a measurement of how high or low the waveform is (which represents how LOUD the sound wave is - or amplitude for you science buffs).
RECORDS IN COMPUTER
Once again you get a series of numbers - say, 36345, 36218, 36154, etc., or in binary, 1000110111111001, 1000110101111010, 1000110100111010, which you can store in your computer to represent the audio waveform.
And if you spit these numbers back out at the same rate you recorded them into a device (called a digital-to-analog converter), PRESTO! you hear the same sound you recorded.
Ahh! a digital recording!
Now, you don't really need to know exactly how this all happens. But understanding the general principles will help you make sense of all the digital recording terms that are tossed around. Coming Next:
ABOUT WILLIAM ...
William Williams is a voice over talent with national, regional and local credits. He has also been a voice over coach in Los Angeles for 15 years where he teaches regular classes, does private coaching, and produces voice over demos at Aliso Creek Productions, in Burbank. He also offers online voice-over classes and coaching.
Email: william@alisocreek.net
Online voice-over classes: http://onlinevoiceoverclasses.com
... Low Prices ... Speedy Delivery!
|
|
|
"Send me a 16 bit 44.1khertz .wav file, a 16 bit 44.1khertz .aiff file to my FTP site and an MP3 file at 160k in an email" 
.png)
I've taken computer classes, and I sort-of understood what they were getting at, but you have taught it like a true teacher. (I should know. I've been a language teacher for years.) You related technical concepts to common, every-day images. Everything made sense to me. Thanks again for sharing yourknowledge.
I've had those requirements set before me by clients, like you have mentioned, which are mostly greek to me. I just send them my standard mp3 or wav file and see what happens. To date, no problems. I sure hope it stays that way!!
For those inclined to tackle the science of sound engineering, I wish you the best of luck.
That very thing happened to me! And I realize you can't make me an instant sound engineer by me reading a few articles. But I can at least have a basic understanding as to how a 16-bit recording is better or worse than a 32-bit recording.
The thing that gets me about "binary code" is how does that number with which we're so familiar - 1,362,478 - actually turn into a binary number like 101001100101000101110? That's the part that confuses me.
Anyway, I look forward to the next lesson!
Larry